The seemingly straightforward task of splitting bills among sharehouse residents in Tokyo conceals layers of mathematical complexity that can transform simple cost-sharing into intricate computational challenges. What appears to be basic arithmetic involving division and proportional allocation evolves into multifaceted problems encompassing variable usage patterns, seasonal fluctuations, currency conversions, and temporal misalignments that test even mathematically inclined residents’ patience and precision.
The mathematical intricacies of bill splitting in shared living environments stem from fundamental assumptions about equal usage and proportional responsibility that rarely align with actual consumption patterns and lifestyle differences among diverse international residents. Understanding utility bills in Japanese sharehouses reveals how these complexities multiply when dealing with Japanese billing systems, seasonal variations, and cultural differences in resource consumption habits.
The Fundamental Mathematics of Unequal Usage
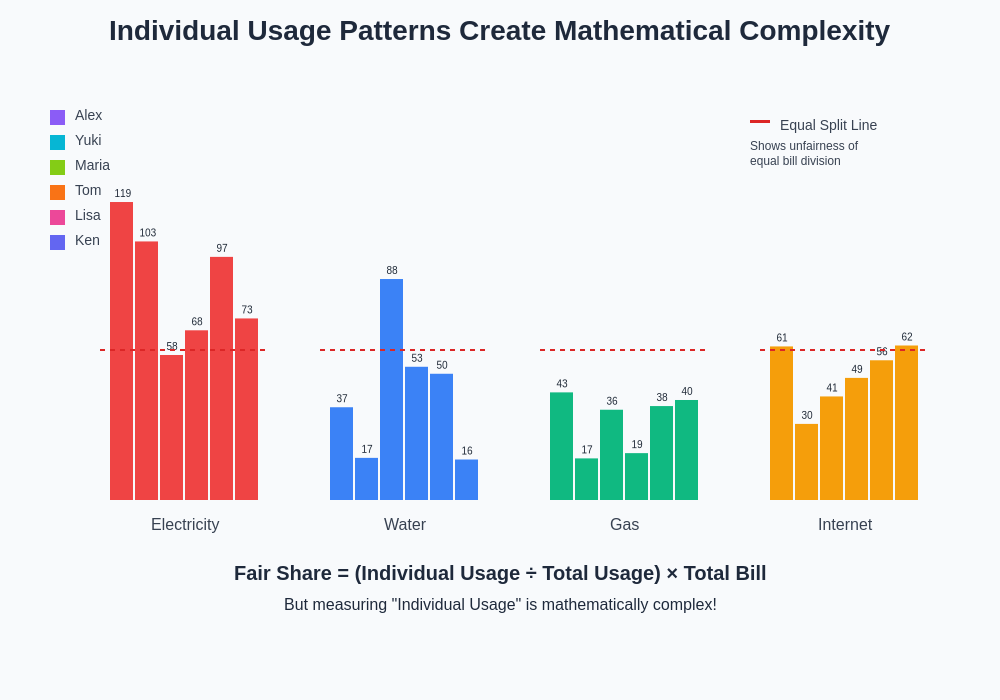
Traditional bill splitting relies on the mathematical premise that equal division represents fair distribution, yet this assumption crumbles when confronted with the reality of dramatically different usage patterns among sharehouse residents. The mathematical challenge begins with establishing baseline consumption levels for each resident across multiple utility categories, requiring complex data collection and analysis that most houses lack the infrastructure or motivation to implement systematically.
Air conditioning usage alone creates exponential complexity in mathematical calculations, as individual thermal comfort preferences, room locations, insulation quality, and occupancy schedules create wildly different energy consumption patterns that resist simple proportional allocation. A resident who maintains their room at eighteen degrees Celsius throughout summer while working from home generates fundamentally different costs than someone who uses minimal cooling and spends most daylight hours outside the sharehouse.
The mathematical modeling required to fairly distribute air conditioning costs involves multiple variables including room size coefficients, usage duration matrices, temperature differential calculations, and seasonal adjustment factors that transform simple division into complex algorithmic challenges. How air conditioning bills spike in summer demonstrates how these seasonal variations can multiply monthly costs by factors of three to five, creating mathematical distribution problems that simple equal splitting cannot address equitably.
Water consumption presents additional mathematical complexities through the intersection of individual usage patterns, shared facility capacity, and time-based pricing structures that many Tokyo utility companies employ. Calculating fair water bill distribution requires tracking individual shower durations, dishwashing frequencies, laundry loads, and cleaning activities while accounting for shared usage of common facilities that benefit all residents regardless of direct participation.
Temporal Displacement and Occupancy Variables
The mathematical complexity of bill splitting intensifies when accounting for temporal displacement of residents whose travel schedules, work patterns, and lifestyle choices create irregular occupancy patterns that traditional equal-splitting methods fail to address accurately. A resident who travels internationally for three weeks each month generates dramatically different utility consumption than someone who works from home daily, yet most sharehouses apply identical cost allocation regardless of actual usage periods.
Mathematical models for fair temporal adjustment require sophisticated algorithms that account for baseline facility costs, variable usage components, occupancy percentages, and seasonal adjustments across multiple billing cycles. How business travel affects house payments explores how professional travel schedules create mathematical inequities in traditional equal-splitting systems.
The calculation of proportional responsibility becomes exponentially complex when multiple residents have overlapping but different absence patterns, requiring matrix calculations that track occupancy intersections, shared facility usage during various occupancy combinations, and baseline cost allocation for maintaining services during partial occupancy periods. These mathematical challenges often exceed the computational capabilities and patience of typical sharehouse residents.
Seasonal employment patterns among international students and working holiday visa holders create additional temporal variables that require mathematical modeling across extended periods rather than simple monthly calculations. A resident who works intensive seasonal jobs with corresponding absence periods followed by extended home occupancy requires mathematical formulas that can accurately distribute costs across irregular time periods while maintaining fairness for consistently present residents.
Currency Conversion and Exchange Rate Fluctuations
International residents in Tokyo sharehouses face additional mathematical complexities when managing bill payments through multiple currencies, creating compound calculation challenges that involve real-time exchange rate monitoring, conversion fee calculations, and temporal arbitrage considerations that can significantly impact individual cost burdens over extended periods.
The mathematical precision required for accurate currency conversion calculations becomes particularly complex when residents pay their portions in different currencies while bills arrive in Japanese yen, requiring continuous exchange rate monitoring and retroactive adjustment calculations that account for conversion timing differences and associated banking fees. How currency exchange affects monthly payments examines how these fluctuations can create unexpected mathematical variations in individual payment obligations.
Exchange rate volatility introduces stochastic mathematical elements that transform predictable monthly budgeting into complex probability calculations involving risk assessment, hedging strategies, and temporal optimization of conversion timing. Residents must navigate mathematical decisions about when to convert currencies, how to minimize conversion costs, and how to distribute exchange rate risks across multiple residents with different currency exposures.
The mathematical modeling required for fair currency conversion cost distribution involves complex algorithms that account for individual currency preferences, conversion frequency optimization, fee sharing protocols, and exchange rate risk allocation across multiple residents with varying financial sophistication and risk tolerance levels.
Proportional Usage Calculation Challenges
Determining fair proportional usage across different types of shared expenses requires mathematical frameworks that can accurately weight various consumption categories while accounting for individual preferences, lifestyle differences, and cultural variations in resource utilization patterns that resist standardized measurement approaches.
Grocery bill splitting presents particularly complex mathematical challenges when residents have dramatically different dietary requirements, cooking frequencies, storage needs, and cultural food preferences that create disproportionate costs across various expense categories. How dietary restrictions complicate meal planning reveals how individual dietary needs can create mathematical inequities in simple equal-splitting systems.
The mathematical complexity increases exponentially when attempting to create fair allocation systems for mixed individual and shared purchases, requiring sophisticated tracking mechanisms that can distinguish personal consumption from communal benefits while accounting for bulk purchase savings, convenience premiums, and quality preference variations that affect overall cost structures.
Cleaning supply and household maintenance expense distribution requires mathematical models that account for individual cleanliness standards, usage patterns of shared facilities, contribution levels to household maintenance activities, and benefit distribution from various cleaning and maintenance expenditures. These calculations involve subjective variables that resist precise mathematical quantification yet significantly impact fair cost distribution.
Seasonal and Variable Rate Complications
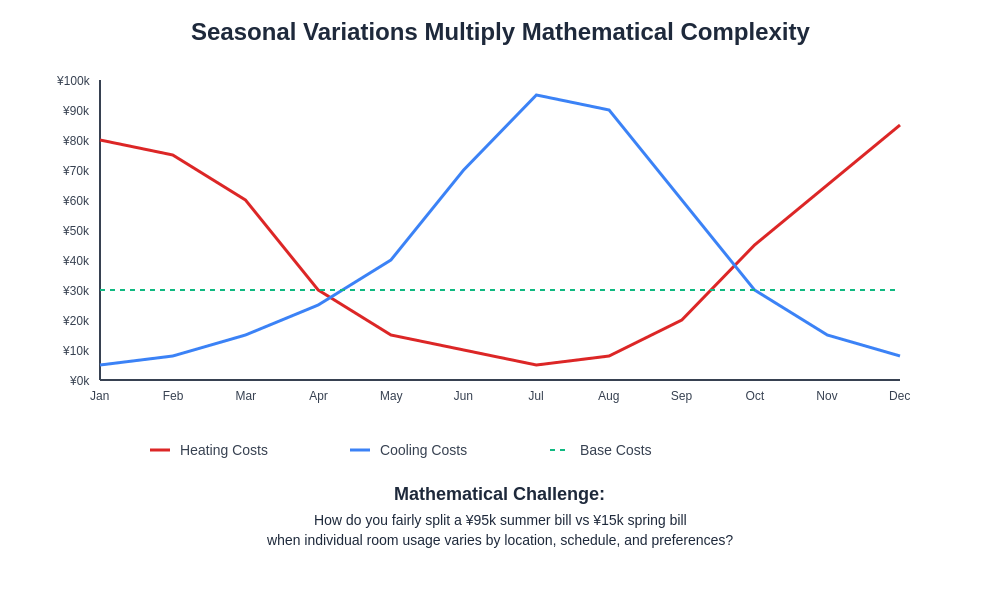
Tokyo’s utility pricing structures incorporate seasonal rate variations, time-of-use pricing, and consumption tier adjustments that create mathematical complexities requiring sophisticated modeling to fairly distribute costs among residents with different usage patterns and schedules. How seasonal demand affects sharehouse prices demonstrates how these variations compound throughout annual cycles.
Winter heating costs present mathematical distribution challenges that involve thermal efficiency calculations, room-specific heating requirements, insulation quality variations, and individual temperature preferences that create exponentially different heating loads across various rooms and usage patterns. The mathematical modeling required for fair heating cost distribution involves complex algorithms accounting for thermal dynamics, usage optimization, and equitable distribution of comfort-related expenses.
Summer cooling costs multiply these mathematical complexities through the interaction of individual thermal comfort preferences, room orientation effects, occupancy schedule variations, and cooling efficiency optimization strategies that create dramatically different cost burdens requiring sophisticated mathematical allocation methods.
Electricity rate tier systems employed by many Tokyo utility companies create additional mathematical complexity through progressive pricing structures that reward conservation while penalizing excessive consumption, requiring mathematical models that can fairly distribute both conservation incentives and excess usage penalties across multiple residents with varying consumption patterns.
Technology Integration and Automation Challenges
Modern sharehouse bill splitting increasingly relies on digital platforms and mobile applications that promise to simplify complex calculations through automation, yet these technological solutions often introduce new mathematical complexities related to data accuracy, algorithm transparency, and system integration challenges that can create unexpected errors and inequities.
Automated bill splitting applications must navigate mathematical challenges related to data synchronization across multiple platforms, real-time usage monitoring, complex rule engine implementation, and user interface design that makes sophisticated mathematical calculations accessible to residents with varying mathematical literacy levels. How shared expense apps create new problems explores how technological solutions can introduce additional mathematical complications.
Smart home technology integration creates opportunities for precise usage monitoring while introducing mathematical challenges related to data interpretation, privacy considerations, system reliability, and integration complexity that can make automated solutions more mathematically complex than manual calculation methods.
The mathematical validation of automated calculation systems requires independent verification methods that can detect algorithmic errors, data corruption, and systematic biases while maintaining user-friendly interfaces that don’t overwhelm residents with computational complexity.

This progression from simple equal splits to complex multi-variable formulas illustrates why most sharehouses struggle to implement fair mathematical solutions that satisfy both accuracy requirements and practical usability constraints.
Psychological and Social Mathematics
The mathematical precision required for fair bill splitting intersects with psychological and social factors that introduce subjective variables resistant to quantitative analysis yet significantly impact resident satisfaction with mathematical allocation methods. Perceived fairness often depends on factors that resist mathematical quantification, creating tension between computational accuracy and social harmony.
Individual financial circumstances create mathematical considerations related to ability to pay, temporary financial hardship accommodation, and equitable burden distribution that require mathematical models incorporating income-based adjustments and flexible payment structures while maintaining overall system fairness and sustainability.
Cultural differences in financial management approaches, privacy expectations, and collective responsibility concepts introduce mathematical variables related to transparency requirements, data sharing protocols, and calculation method preferences that must be integrated into functional mathematical frameworks that satisfy diverse cultural expectations.
Group decision-making processes for establishing mathematical allocation methods require consensus-building approaches that can incorporate multiple perspectives on fairness while maintaining mathematical rigor and practical implementation feasibility across diverse international resident communities.
Advanced Mathematical Solutions and Frameworks
Sophisticated mathematical approaches to fair bill splitting involve algorithmic solutions incorporating multiple optimization criteria, constraint satisfaction methods, and dynamic adjustment mechanisms that can adapt to changing circumstances while maintaining mathematical precision and practical usability for typical sharehouse residents.
Linear programming applications can optimize cost distribution across multiple variables while satisfying fairness constraints, though implementation requires mathematical expertise that exceeds typical sharehouse resident capabilities. How to budget realistically for sharehouse living provides practical frameworks for managing these mathematical complexities.
Game theory applications offer mathematical frameworks for analyzing strategic interactions among residents seeking to optimize individual cost burdens while maintaining group cooperation and system sustainability. These mathematical models can provide insights into optimal sharing strategies while identifying potential conflicts and resolution mechanisms.
Statistical analysis methods can identify patterns in consumption data that enable predictive modeling for future cost distribution while accounting for seasonal variations, occupancy changes, and usage pattern evolution over extended periods.
Practical Implementation Strategies
Successful mathematical bill splitting implementation requires practical frameworks that balance computational accuracy with usability constraints while maintaining flexibility for diverse resident needs and changing circumstances. The mathematical sophistication must be hidden behind user-friendly interfaces that make complex calculations accessible to residents with varying mathematical backgrounds.
Establishing mathematical protocols for handling exceptional circumstances, dispute resolution, and system adjustment ensures that sophisticated mathematical frameworks remain functional when confronted with real-world complications and resident conflicts. How to handle roommate conflicts without moving out provides guidance for managing mathematical disagreements constructively.
Regular mathematical auditing and adjustment procedures ensure that complex allocation systems maintain accuracy and fairness over time while adapting to changing resident compositions, usage patterns, and external factors that affect mathematical model validity.
Training and education programs that help residents understand mathematical allocation principles can improve acceptance and cooperation while reducing conflicts related to perceived unfairness or computational errors in complex mathematical systems.
The mathematical complexity of bill splitting in Tokyo sharehouses reflects broader challenges in fair resource allocation among diverse groups with varying needs, preferences, and circumstances. Successful navigation requires mathematical sophistication combined with practical wisdom and social sensitivity that recognizes the limits of pure mathematical solutions in complex social environments.
Disclaimer
This article is for informational purposes only and does not constitute financial or mathematical advice. Bill splitting methods should be agreed upon by all residents and may require professional consultation for complex situations. The mathematical approaches discussed may not be suitable for all sharehouse arrangements, and individual circumstances may require customized solutions.
